Demystifying the Derivative of Sin: A lighthearted trip down Calculus lane
5 min read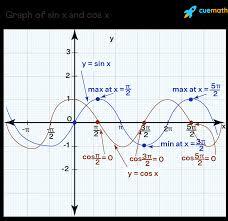
Demystifying the Derivative of Sin: A lighthearted trip down Calculus lane
This is the first in a series of posts where we’ll take an exciting journey on calculus-land and talk about one of its most fascinating mathematical creations, which gives birth to many important concepts: The Sine Function. But, right now — I know what your thinking: “oh no not another derivatives one“. Just pause. We are going to break this down and, for lack of a better word — play.
What is a Derivative Anyway?
I want you to imagine for a minute that you are on the road traveling somewhere. You are behind the wheel of course, and you need to always know your current speed. Learn the speedometer. Your only friend is that sucker because it tells you how fast your position changes (your velocity). In the language of calculus, getting your rate of change (in this case how fast you are moving down the road) is called taking a derivative.
What that means is, taking the derivative of a function makes us another function which tells you how quick the original one changes. For instance if you were on an amusement park ride like a roller coaster, the rate of change (or derivative) of your height as a function over time will inform how quickly up or down you are rising.
Introducing Sin(x) : The Curvy Function
The sine function (sin(x)) is probably on of the most interesting functions in mathematics. It creates a regular, undulating curve that resembles rolling hills for as far as the eye can see. I like to describe it as the functional form of a rhythmic dance: up and down in ebbs.
Okay, So What is the Derivative of Sin(x)?
If you were wishing that sin(x)\sin(x)sin(x) would be a weirdo and its derivative, hope again. The derivative of sin(x)\sin(x)sin(x) is as trustworthy your grandma’s apple pie recipe. And the answer is… cos(x)cos(x)cos(x).….. Wait for it….
Yes, you read that right. Derivative of sin(x) = cos(x). Therefore, whenever you got sin(x)\sin(x)sin(x), the derivative will always be cos(x)\cos(x)cos(x). Think of it as the best dance partner, wherever sin(x)sin(x)sin(x) goes cos(x)\cos(x)\cos x follows. It also does not have stage fright — always prepared to maintaining the beat.
But, Why is ∂(sin(x))/∂x = cos(x)
Okay, let us go slightly below the surface. The famous function that resembles a wave is the sine function. While sin(x)sin(x)… are analogous to a gentle ocean wave, think instead of cos(x)\cos(x)cos(x), as how the water curls over immediately once it hits the beach. At the peak (highest point) of each sine wave, the cosine is just crossing “0” or x-axis. When sin(x)\sin(x)sin(x) is at its minimum (trough), cos(x)\cos(x)cos(x)=θ \theta θ.
This derivative cos(xcos(x)cos(x), that is to say, the fact sin'(x)=cosby calculus means how does sin reflect around every point which can be represented mathematically as a number. If sin(x)\sin(x)sin(x) is increasing, that means cos(x)>0\cos(x)>0cos(x)>0 and the slope isn’t going downwards. If sin(x)sin(x)sin(x)>0, cin(x)
Putting This (Kind Of) In Perspective
This is the easiest way to think about it(Image Source: lovelace. The hula hoop will not sit still at one height above the ground (which you might think of as sin(x)\sin(x)sin(x))Mathf sincosinesinecosinsin () ()) changes as they rotate. The area corresponds to the rate at which height changes btw, this is why you take a derivative for it but how fast does that hight change (which itself in sence of movement) will given by how quickly bakwas moves up or down. That’s where cos(x)\cos(x) comes from
To be quick, the height of the hoop when viewed in front is somewhat captured by a sine function and how quickly it moves up or down (pointing outwards) which translates to cosine. The hoop is in constant communion with itself, speed and height dancing together to perfection.
A Little Humour — Derivative Drama
How about a little story to break the tension?
In prep math fantasy land, there was this function called Sine. Sine was a pendulum which ceaselessly swung back and forth, sculpting perfect waves. The day arrived when Sine meets Cosine at a function party. “Hey, Cosine! Here I am, making some pretty big waves today.. What about you?”
Ans: Oh Sine, you know me. Please remember that I will be there for you. Just like your derivative!”
Sine looked puzzled. “Derivative? What do you mean?”
Cosine grinned. “Yeah, every time you wave up or down I come right in and tell the world how tall this total tidal bullshit tsunami is. Mae: [Laughs] We are the math world dynamic duo!
And so, Sine and Cosine danced back and forth forever knowing that they were meant for one another: One moved to mirror the sway of other A beautiful and harmonious relationship, proving that even in math there is a place for leisure activities together.
Interactive Visualization of Derivatives
I highlight the graphs that provide excellent visualization to see how functions and their derivatives interact…and just do it. When you plot sin(x)\sin(x)sin(x) and cos(x)\cos(x)cos(x), however, it is like they are dancing:
sin(x)sin(x)sin(x)y sin goes from 0 to 1 back down at -1 then comes right back up.
cos(x) cos(x)= 1, -1….
The key takeaway? At the top or bottom of sin(x)\sin(x)sin(x), cos(x)=0\cos ( x ) = 0cos(x)=0 crosses it. Sin(x)\sin(x) sin when crossing 0, then cos( x ) \cos (x) c o s will peak and trough. Like a perfectly choreographed dance move they are always in sync.
Applications and Fun Facts
The applications of Derivatives are not bound to Academics! They are used by engineers to create a cozy ride in roller coasters as well as physicists study them oscillations and waves. And when music producers adjust the shape of sound waves are they performing not too similar math?
Fun fact: when next you are humming a tune, and it feels like the flow in it is your favorite part (rhythm), that might just be derivatives at work!!! Music and calculus: who knew?
Final Thoughts
And so it is, this frothy fact: the derivative of sin(x)\sin(x)sin(x), to speak mathematically and sensuously at once — a reliable as your first solid espresso on Monday morning. This relationship between sin(x)\sin(x)sin(x) and cos(x)\cos(x)cos(x), which I hope you internalized, gives us a catalyst for exploring broader mathematical ideas as well real-world applications:
Calculus does not have to be all that intimidating, either. Some imagination and a little humor can make even the most abstract concepts accessible, mentally attractive. So the next time you meet sin(x)\sin(x)sin(x) and its faithful companion cos(x), give them little shout-out for all the mathematical break dancing they do!