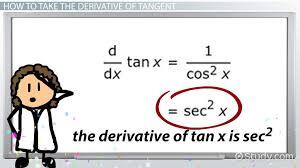
Understanding the Derivative of Tan: A Fun and Friendly Guide

When you first encounter the tangent function in calculus, you might think of it as a wild party guest who never stops talking. Its derivative can be equally rambunctious if you don’t handle it right. But fear not! This guide will break down the derivative of $tan⁡(x)\tan(x)$ with a dash of humor and simplicity. So, grab a coffee, put on your math hat, and let’s dive into the world of derivatives with a smile on our faces.

What’s the Deal with Tangent?

Before we talk derivatives, let’s get to know our function better. The tangent function, $tan⁡(x)\tan(x)$ , is like the enthusiastic friend who can’t stay in one place. It cycles through values and keeps going up and down as $x$ increases. If you’ve ever seen a graph of $tan⁡(x)\tan(x)$ , you know it looks like a roller coaster—except with a lot more asymptotes and fewer safety restraints.

Mathematically, $tan⁡(x)\tan(x)$ is defined as:

$tan⁡(x)=sin⁡(x)cos⁡(x)\tan(x) = \frac{\sin(x)}{\cos(x)}$

In plain English, it’s the ratio of the sine function to the cosine function. But just like dividing by zero is a bad idea, the tangent function hits some snags where the cosine function equals zero, causing those wild asymptotes we mentioned. These occur at $\frac{\pi}{2} + n\pi$ , where $n$ is an integer. At these points, the tangent function behaves like your overly caffeinated friend who suddenly jumps on a trampoline—things get a bit crazy!

The Derivative of Tan(x): The Grand Reveal

Now, onto the heart of the matter: finding the derivative of $tan⁡(x)\tan(x)$ . The derivative is like the speedometer of a function, telling us how fast it’s changing at any given point. For $tan⁡(x)\tan(x)$ , the derivative has its own flair, and it’s as follows:

$ddxtan⁡(x)=sec⁡2(x)\frac{d}{dx} \tan(x) = \sec^2(x)$

You might be thinking, “Whoa, that’s a lot of letters!” But don’t worry; it’s not as intimidating as it looks. Let’s break it down:

Secant Function: The secant function, $sec⁡(x)\sec(x)$ , is the reciprocal of the cosine function. In other words: $sec⁡(x)=1cos⁡(x)\sec(x) = \frac{1}{\cos(x)}$
So, $sec^2(x)$ is simply:

$sec⁡2(x)=(1cos⁡(x))2=1cos⁡2(x)\sec^2(x) = \left( \frac{1}{\cos(x)} \right)^2 = \frac{1}{\cos^2(x)}$
Why Secant?: To understand why the derivative of $tan⁡(x)\tan(x)$ is $sec^2(x)$ , let’s get a bit technical. The tangent function is a bit of a complicated beast, and its rate of change is influenced by how the sine and cosine functions are behaving. By taking the derivative, we essentially see that as the tangent function grows, it does so at a rate proportional to $sec^2(x)$ .If that sounds like a mouthful, here’s a simpler analogy: if the tangent function were a car, its speed (derivative) depends on the curvature of the road (secant squared). The sharper the turn, the faster you’re going!

Why Is This Useful?

Understanding the derivative of $tan⁡(x)\tan(x)$ is more than just a party trick for calculus. It has practical applications in various fields:

Physics: In physics, especially in wave mechanics and oscillations, understanding how functions change is crucial. The derivative of $tan⁡(x)\tan(x)$ helps model and solve problems involving angular motion and acceleration.
Engineering: Engineers often deal with trigonometric functions when designing curves and systems. Knowing how the tangent function behaves helps in optimizing designs and predicting system behavior.
Everyday Life: Okay, you might not need this at your next dinner party, but if you’re into optimizing anything (like the angle of your bike ramp for maximum fun), understanding these derivatives is handy.

Visualizing the Derivative

Let’s add some color to our understanding with a graph. Imagine the graph of $tan⁡(x)\tan(x)$ . It’s a roller coaster that goes up and down and has vertical asymptotes where it goes to infinity. The graph of $sec^2(x)$ , on the other hand, is like a series of hills—its shape mimics the tangents’ highs and lows, but without the asymptotes.

If you were to plot these on the same axes, you’d see that wherever $tan⁡(x)\tan(x)$ is climbing steeply, $sec^2(x)$ is giving you the exact rate of that climb. Conversely, when $tan⁡(x)\tan(x)$ levels off, $sec^2(x)$ is low. It’s like having a speedometer that tells you how fast the roller coaster is zooming through its ups and downs.

Common Missteps and How to Avoid Them

Forget the Asymptotes: Sometimes, students forget that $tan⁡(x)\tan(x)$ has vertical asymptotes. These are not just decorative lines; they’re crucial because $tan⁡(x)\tan(x)$ becomes undefined here. Make sure you account for these in your calculations and avoid trying to find derivatives at these points.
Secant Confusion: The secant function can be confusing because it’s not as commonly used as sine or cosine. Remember, $sec⁡(x)\sec(x)$ is simply $1cos⁡(x)\frac{1}{\cos(x)}$ . So, when you see $sec^2(x)$ , just square the reciprocal of cosine.
Unit Circle Mayhem: If you’re using the unit circle to understand these functions, ensure you’re clear on which quadrant you’re in. The values of $sin⁡(x)\sin(x)$ and $cos⁡(x)\cos(x)$ change depending on the quadrant, and this affects $tan⁡(x)\tan(x)$ and $sec^2(x)$ accordingly.

A Quick Example

Let’s put this into practice with a quick example. Suppose you have a function $\tan(x)$ and you want to find the derivative at $\frac{\pi}{4}$ .

Calculate $sec^2(x)$ at $\frac{\pi}{4}$ :
- At $\frac{\pi}{4}$ , $cos⁡(x)=22\cos(x) = \frac{\sqrt{2}}{2}$ .
- Therefore, $sec⁡(x)=122=2\sec(x) = \frac{1}{\frac{\sqrt{2}}{2}} = \sqrt{2}$ .
- Thus, $sec⁡2(x)=(2)2=2\sec^2(x) = (\sqrt{2})^2 = 2$ .
So, the derivative of $tan⁡(x)\tan(x)$ at $\frac{\pi}{4}$ is 2.

This means that at $\frac{\pi}{4}$ , the tangent function is increasing at a rate of 2 units per unit of $x$ . Not bad for a quick calculation!

Wrapping Up

Understanding the derivative of $tan⁡(x)\tan(x)$ can seem like trying to tame a wild beast at first, but with a bit of practice, you’ll find it’s really just another function with its own quirks and patterns. Remember, the derivative of $tan⁡(x)\tan(x)$ is $sec^2(x)$ , which tells you how the tangent function is changing at any given point. It’s like having a speedometer for our roller coaster of a function!

So next time you encounter $tan⁡(x)\tan(x)$ , don’t let it scare you. Just remember: it’s all about how fast it’s changing, and with $sec^2(x)$ in hand, you’ll be able to keep up with its wild ride. Happy differentiating!